Answer:
C
Explanation:
We want to integrate:
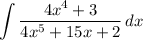
Notice that the expression in the denominator is quite similar to the expression in the numerator. So, we can try performing u-substitution. Let u be the function in the denominator. So:
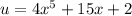
By differentiating both sides with respect to x:
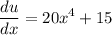
We can "multiply" both sides by dx:
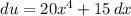
And divide both sides by 5:
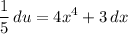
Rewriting our original integral yields:
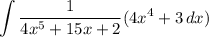
Substitute:
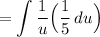
Simplify:
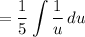
This is a common integral:
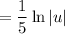
Back-substitute. Of course, we need the constant of integration:
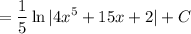
Our answer is C.