Question

Yea I do agree that with this one ☝️ I will be coming

Answer 1

- The equation for the potential given is:

`V(t)=320e^(-3.1t)`

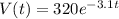
Question 1:

- To find when the potential is 150V, we simply substitute the value of V = 150 into the equation and then find the corresponding value of t.

- Thus, we have:

`\begin{gathered} V=150 \\ \\ 150=320e^(-3.1t) \\ \\ \text{ Divide both sides by 320} \\ \\ e^(-3.1t)=(150)/(320)=(15)/(32) \\ \\ \text{ Take the natural log of both sides} \\ \\ \ln e^(-3.1t)=\ln((15)/(32)) \\ \\ -3.1t=\ln((15)/(32)) \\ \\ \text{ Divide both sides by -3.1} \\ \\ t=-(1)/(3.1)\ln((15)/(32)) \\ \\ t=0.2444s\text{ \lparen To 4 decimal places\rparen} \end{gathered}`

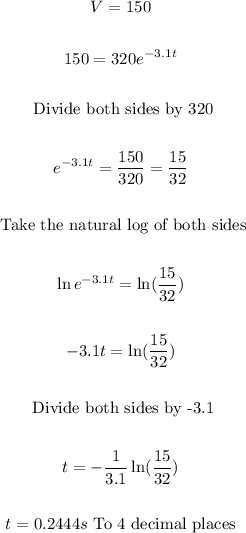
Question 2:

- The rate at which the changing occurs is gotten by differentiating the function with respects to time.

- That is,

`\begin{gathered} V(t)=320e^(-3.1t) \\ \\ V^(\prime)(t)=(d)/(dt)(320e^(-3.1t)) \\ \\ V^(\prime)(t)=320(-3.1e^(-3.1t)) \\ \\ V^(\prime)(t)=-992e^(-3.1t) \end{gathered}`

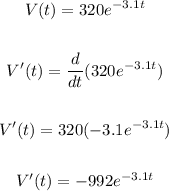
- Now that we have the expression for the rate of change of potential with time, we can proceed to find how fast the changing of potential V is happening at t = 0.2444s.

- Thus, we have:

`\begin{gathered} V^(\prime)(t)=-992e^(-3.1t) \\ put\text{ }t=0.2444 \\ \\ V^(\prime)(t)=-992e^(-3.1*0.2444) \\ \\ \therefore V^(\prime)(t)=-465.02125...\approx-465.0\text{ v/s} \end{gathered}`

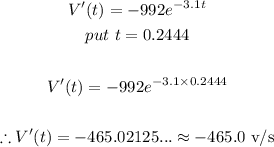
Question 3:

- The voltage is changing at -50v/s when we substitute V'(t) = -50 into the equation for V'(t).

- We have that:

`\begin{gathered} V^(\prime)(t)=-992e^(-3.1t) \\ \\ V^(\prime)(t)=-50 \\ \\ -50=-992e^(-3.1t) \\ \\ \text{ Divide both sides by -992} \\ \\ e^(-3.1t)=(-50)/(-992)=(25)/(496) \\ \\ \text{ Take the natural log of both sides} \\ \ln e^(-3.1t)=\ln((25)/(496)) \\ \\ -3.1t=\ln((25)/(496)) \\ \\ \text{ Divide both sides by -3.1} \\ \\ \therefore t=-(1)/(3.1)\ln((25)/(496)) \\ \\ t=0.96377...\approx0.9638seconds\text{ \lparen To 4 decimal places\rparen} \end{gathered}`

Final Answers

Question 1: 0.2444 seconds

Question 2: -465.0v/s

Question 3: 0.9638 seconds