Question

Write a coordinate proof: Given: Coordinates of triangle DEF, H is the midpoint of DA, G is the midpoint of EA . Prove: Side DG is congruent to side EH Here is the image down below. I have to fill in the blanks with each of the correct choices that are provided down below.

Answer 1

Consider the image in the below

From the diagram above,

`\begin{gathered} H\text{ is the mid point of AD} \\ \text{And } \\ G\text{ is the midpoint of AE} \end{gathered}`

Then we obtain the coordinate of H and G

Using the coordinate of midpoint formula,

`\begin{gathered} \text{Coordinate of H is } \\ (-(2h+0)/(2),(2k+0)/(2))=((-2h)/(2),(2k)/(2))=(-h,k) \end{gathered}`

Then

`\begin{gathered} \text{Coordinate of G } \\ ((2h+0)/(2),(2k+0)/(2))=((2h)/(2),(2k)/(2))=(h,k) \end{gathered}`

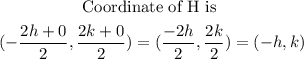
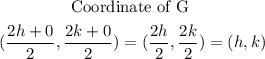
Then use the distance formula to fined the lenght of |EH| and |DG|

The Distance formula is given by

`\text{Distance}=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}`

Hence

`\begin{gathered} U\sin g\text{ the coordinatesH= (-h,k) and E= (2h,0) } \\ \text{Then} \\ |EH|=\sqrt[]{(2h-(-h)^2+(0-k)^2} \\ |EH|=\sqrt[]{(3h)^2+(-k)^2} \\ \text{Then } \\ |EH|=\sqrt[]{9h^2+k^2} \end{gathered}`

Then

`\begin{gathered} \text Using the coordinatesG= (h,k) and D=(-2h,0) for \\ |DG|\text{ =}\sqrt[]{(-2h-h)^2+(0-k)^2} \\ |DG|=\sqrt[]{(-3h)^2^{}+(-k)^2} \\ \text{hence } \\ |DG|-=\sqrt[]{9h^2+k^2} \end{gathered}`

Hence

Since we obtain the same expression above

Then

`\begin{gathered} |EH|=|DG| \\ or \\ |DG|=|EH| \end{gathered}`

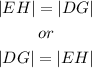
therefore

`|DG|\cong|EH|`

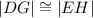
Therefore

Answer: DG is congruent to side EH