Question

Write a system of equations to describe the situation below, solve using an augmented matrix, and fill in the blanks.Barbara is a salon owner. Yesterday, she did 1 haircut and colored the hair of 3 clients, charging a total of $253. Today, she did 1 haircut and colored the hair of 5 clients, charging a total of $399. How much does Barbara charge for her services?Barbara charges $ for a haircut and $ for a coloring.

Answer 1

the charges for a haircut is $34

hence, the charges for a coloring is $ 73

Step-by-step explanation

Step 1

set the equations.

a) let x represents the charges for one haircut

let y represents the charges for one coloring

b) translate into math terms

i) she did 1 haircut and colored the hair of 3 clients, charging a total of $253,so

`x+3y=253\Rightarrow equation(1)`

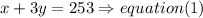
ii)Today, she did 1 haircut and colored the hair of 5 clients, charging a total of $399. so

`x+5y=399\Rightarrow equation(2)`

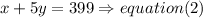
Step 2

Solve the equations:

a) isolate the x value in equation (1) and replace the value into equation(2)

`\begin{gathered} x+3y=253\Rightarrow equation(1) \\ subtract\text{ 3y in both sides} \\ x+3y-3y=253-3y \\ x=253-3y \end{gathered}`

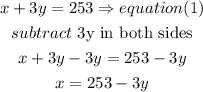
replace in equation (2)

`\begin{gathered} x+5y=399\Rightarrow equation(2) \\ (253-3y)+5y=399 \\ add\text{ like terms} \\ 253+2y=399 \\ subtract\text{ 253 in both sides} \\ 253+2y-253=399-253 \\ 2y=146 \\ divide\text{ both sides by 2} \\ (2y)/(2)=(146)/(2) \\ y=73 \end{gathered}`

hence, the charges for a coloring is $ 73

b), now replace the y value into equation (1) and solve for x

`\begin{gathered} x+3y=253\Rightarrow equation(1) \\ x+3(73)=253 \\ x+219=253 \\ x=34 \end{gathered}`

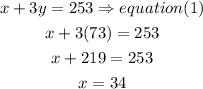
therefore,

the charges for a haircut is $34

I hope this helps you

.