Given data:
* The force applied on the block is,
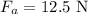
* The frictional force acting on the block is,
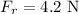
* The acceleration of the block is,
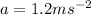
Solution:
The net force acting on the block is,
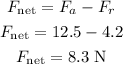
According to Newton's second law, the net force in terms of the mass and acceleration of the block is,
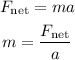
Substituting the known values,
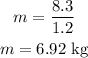
As the block is initially at rest, thus, the initial speed of the block is u = 0 m/s.
By the kinematics equation, the final speed of the block after t = 5 seconds is,
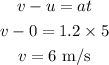
Thus, the final speed of the block after t = 5 seconds is 6 meters per second.
The kinetic energy of the block after t = 5 seconds is,
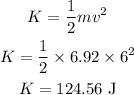
Thus, the kinetic energy of the block after t = 5 seconds is 124.56 joule.