Question

Consider the equation: x2 + 10x + 9 = 0 = E and A) First, use the "completing the square" process to write this equation in the form (x + D)? enter your results below. x2 + 10x + 9 = 0 is equivalent to: Preview left side of eqn: B) Solve your equation and enter your answers below as a list of numbers, separated with a comma where necessary. Answer(s):

Answer 1

-1, -9

Step-by-step explanation:

Given the expression;

`x^2+10x+9=0`

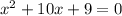
To apply the completing the square method;

First, subtract 9 from both sides

`\begin{gathered} x^2+10x+9-9=0-9 \\ x^2+10x=-9 \end{gathered}`

Complete the square by adding the half of the square of the coefficient of x to both sides of the expression as shown;

`\begin{gathered} x^2+10x+((10)/(2))^2=-9+((10)/(2))^2 \\ x^2+10x+(5)^2=-9+(5)^2 \\ (x+5)^2=-9+25 \\ (x+5)^2=16 \end{gathered}`

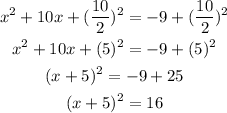
Next is to find the values of x by squaring both sides of the expression;

`\begin{gathered} \sqrt[]{(x+5)^2}=\pm\sqrt[]{16} \\ x_{}+5=\pm4 \\ x+5\text{ = 4 and x+5=-4} \\ x\text{ = 4-5 and x = -4-5} \\ x\text{ = -1 and x =-9} \end{gathered}`

Hence the values of x are -1 and -9