The given information is:
- The average test score is 85 points
- The standard deviation is 9
- It is a normal distribution
We need to find the best estimate for the proportion of students earned a 70 points or higher.
First, we need to find the z-score for 70, by applying the following formula:

Then, as x=70, we replace the given values and find z:
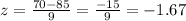
Then, we can find the estimate as follows:
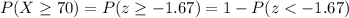
Now, in a standard normal table, we search the cumulative probability of z<-1.67, and it is 0.0475:
Thus, replace this value to find P(X>=70):
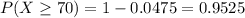
The probability is 0.9525, if we multiply it by 100%, we obtain: 95.25%
The best estimate is 95%.