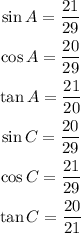Remember that on a right triangle, the trigonometric ratios of a given angle are defined as follows:

On the given figure, the side opposite to the angle C has a length of 20, the side adjacent to C has a length of 21, and the hypotenyse has a lenght of 29.
On the other hand, the side opposite to the angle A has a length of 21, the side adjacent to the angle A has a length of 20 and the hypotenuse is the same.
Then: