Question

Greg walks on a straight road from his home to a convenience store 3.0 km away with a speed of 6.0 km/h. On reaching the store he finds that the store is closed, he instantly turns around and walks back with a speed of 9.0 km/h. Round your final answers to 2 significant figures.b. Find the magnitude of Greg’s average velocity and speed in the time interval from 0 to 50 minutes.

Answer 1

Given:

The distance between home and the store is d = 3 km

The speed to reach the store is v1 = 6 km/h

The speed to travel back the home is v2 = 9 km/h

To find the magnitude of average velocity and speed in the time interval of0 to 50 minutes.

Step-by-step explanation:

The magnitude of average velocity is zero as the displacement is zero.

The average speed can be calculated by the formula

`v_(av)=\frac{total\text{ distance }}{total\text{ time}}`

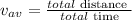
First, we need to calculate time in order to calculate the average speed.

The time taken to reach the store is

`\begin{gathered} t1\text{ =}(d1)/(v1) \\ =\frac{3\text{ km}}{6\text{ km/h}} \\ =(1)/(2)\text{ h} \\ =\text{ 30 minutes} \end{gathered}`

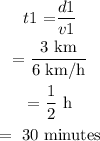
After 30 minutes, the speed is 9 km/h, and the time left is 50 -30 = 20 minutes.

So the distance travelled in the remaining 20 minutes is

`\begin{gathered} d2\text{ =v2}* t2 \\ =9km\text{ /h}*20minutes*\frac{1h}{60\text{ minutes}} \\ =\text{ 3km} \end{gathered}`

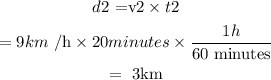
So, the distance travelled is d= d1+d2 = 3+3 = 6km

The total time taken is t = 50 minutes.

Thus, the average speed will be

`\begin{gathered} v_(av)=\frac{6\text{ km}}{50\text{ minutes}}*\frac{60\text{ minutes}}{1\text{ h}} \\ =\text{ 7.2 km/h} \end{gathered}`

Final Answer:

The magnitude of average velocity is zero.

The magnitude of the average speed is 7.2 km/h