Given:
A bacteria culture is started with 200 bacteria.
After 4 hours, the population has grown to 769 bacteria.
the population grows exponentially according to the formula:
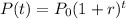
(a) Find the growth rate.
so, when:
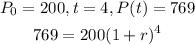
Solve for r:
![\begin{gathered} (769)/(200)=(1+r)^4 \\ 3.845=(1+r)^4 \\ \sqrt[4]{3.845}=1+r \\ 1+r=1.4 \\ r=1.4-1=0.4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/df8cbkat7yhys7vznye1iac4jyj1sz92ps.png)
So, the value of r = 0.4 = 40%
The growth rate = r = 40%
(b) If this trend continues, how many bacteria will there be in one day?
For one day, t = 24 hours
so,
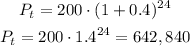
Bacteria = 642,840
(c) How long will it take for this culture to triple in size?
So,
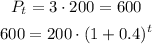
Solve for t:
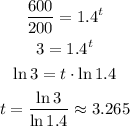
Round your answer to the nearest tenth of an hour.
So, t = 3.3 hours