Question

Solve the statistics question shown in the picture provided, complete A, B, and C, thanks.

Answer 1

a) The variable of interest is X: the price of a home of a certain city.

The distribution of the home prices of the city is strongly skewed right, with mean μ=420 thousand dollars, and standard deviation σ= 180 thousand dollars.

There was a sample of n=60 houses for sale taken, to determine the shape of the sampling distribution you have to apply the Central Limit Theorem, which states:

As a rule, a sample size greater than or equal to 30 is considered sufficient to apply the theorem and use the approximation. So, by applying the CLT you can approximate the sampling distribution to normal:

`X\lbrack bar\rbrack\approx N(\mu,(\sigma^2)/(n))`

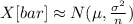
For this example, the distribution is:

`\begin{gathered} X\lbrack bar\rbrack\approx N(420;(32400)/(60)) \\ X\lbrack bar\rbrack\approx N(420;540) \end{gathered}`

b) You have to determine the approximate probability that the mean price of the homes for the sample taken is more than 450 thousand dollars.

To determine this probability you have to work with the approximation of the standard normal distribution, derived from the approximation of the sampling distribution:

`Z=\frac{X\lbrack bar\rbrack-\mu}{\frac{\sigma}{\sqrt[]{n}}}\approx N(0,1)`

You can symbolize the probability as follows:

`P(X\lbrack bar\rbrack>450)=1-P(X\lbrack bar\rbrack\leq450)`

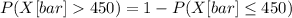
First step is to determine the Z-value corresponding to X[bar]≤450

`\begin{gathered} Z=\frac{X\lbrack bar\rbrack-\mu}{\frac{\sigma}{\sqrt[]{n}}} \\ Z=\frac{450-420}{\frac{180}{\sqrt[]{60}}} \\ Z=\frac{30}{6\sqrt[]{15}} \\ Z=1.29 \end{gathered}`

Using the tables of the standard normal distribution you can determine the probability for values less than or equal to Z=1.29

`P(Z\leq1.29)=0.9010`

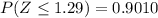
Now you can determine the probability:

`\begin{gathered} P(X\lbrack bar\rbrack>450)=1-P(X\lbrack bar\rbrack\leq450) \\ P(Z>1.29)=1-P(Z\leq1.29)=1-0.9010=0.090 \end{gathered}`

The probability that the mean value of the homes is more than 450 thousand dollars is 0.09 or 9%

c) The probability of obtaining a mean price greater than 450 thousand dollars is 9%, this probability is low, which means that the mean price is an uncommon value.