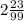Question

A manufacturer determines that the cost of making a computer component is $2.232323.... Write the repeating decimal cost as a fraction and as a mixed number.

Answer 1

Consider that it is mentioned that the number is a repeating decimal. So the cost value can be written as,

`2.\bar{23}`

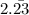
Let this number be 'x',

`\begin{gathered} x=2.\bar{23} \\ x=2.232323\ldots \end{gathered}`

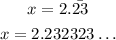
Multiply both sides by 100, since there are 2 digits repeating after the decimal,

`\begin{gathered} 100x=223.\bar{23} \\ 100x=223.232323\ldots \end{gathered}`

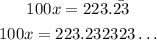
Subtracting the equations,

`\begin{gathered} 100x-x=223.\bar{23}-2.\bar{23} \\ 99x=223+0.\bar{23}-(2+0.\bar{23}) \\ 99x=223+0.\bar{23}-2-0.\bar{23} \\ 99x=221+0 \\ x=(221)/(99) \end{gathered}`

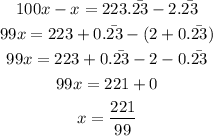
Thus, the fraction corresponding to the repeating decimal is 221/99.

And the corresponding mixed fraction can be evaluated as follows,

`(221)/(99)=(198+23)/(99)=(2(99)+23)/(99)=2(23)/(99)`

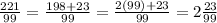
Thus, the mixed fraction corresponding to the repeating decimal will be,

`2(23)/(99)`