Question

Ths rest of the answers that cut off are: -5, 8, -4, 9, -3, -2, -1 ,10 ,11 ,12 Please tell me answer qnd explain how to solve it :)

Answer 1

`\begin{gathered} \text{Let the quadractic function be } \\ y=x^2+bx+c \end{gathered}`

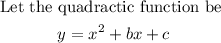
Given that the zeros of the function are at x= 2 and x=6

`\begin{gathered} \text{When x=2, we have} \\ 0=2^2+b(2)+c \\ 0=4+2b+c \\ 2b+c=-4--------\text{equation (1)} \end{gathered}`
`\begin{gathered} \text{When x = 6, we have} \\ 0=6^2+b(6)+c \\ 0=36+6b+c \\ 6b+c=-36-------------\text{equation}(2) \end{gathered}`

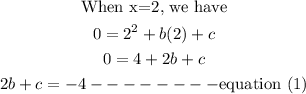
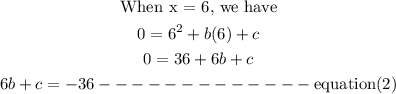
Solving both equations by elimination method, we have

2b + c = -4

6b+c = -36

2b + c-(6b+c)= -4 - (-36)

2b + c-6b-c=-4+36

-4b = 32

b= 32/-4

b= -8

put b= -8 into equation (1)

2b + c = -4

2( -8) + c = -4

-16 + c = -4

c= -4 + 16

c = 12

The function is

`f(x)=x^2-8x+12`

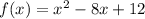
The first missing value is -8, while the second missing value is 12