1 Answer

Randall Goodwin · Answer 1 · 2023-08-18T17:13:40+0000

Mean

Let the number of defects be "x" and probabilities be "p".

We calculate the mean by taking the sum of the products of the number of defects and each of their probabilities. Shown below:

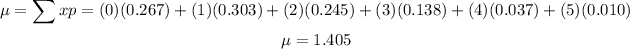
$\begin{gathered} \mu=\sum xp=(0)(0.267)+(1)(0.303)+(2)(0.245)+(3)(0.138)+(4)(0.037)+(5)(0.010)_{} \\ \mu=1.405 \end{gathered}$

Rounding to 1 decimal place

Mean = 1.4

Variance

The formula is:

$\begin{gathered} \sigma^2=\sum (x-\mu)^2\cdot P \\ \sigma^2=(0-1.405)(0.267)+(1-1.405)(0.303)+(2-1.405)(0.245)+(3-1.405)(0.138)+(4-1.405)(0.037)+(5-1.405)(0.010) \\ \sigma^2=0 \end{gathered}$

The variance is 0.

Standard Deviation

The standard deviation is the square root of the variance.

So,

$\sigma=\sqrt[]{\sigma^2}=\sqrt[]{0}=0$

The standard deviation is 0.

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions