Given:
Principal (Investment) = $20,000
Interest Rate = 5.5% or 0.055 in decimal form
Time = 10 years
Compounding period = quarterly = 4 in every year
Find: the accrued amount or final amount after 10 years with interest
Solution:
To find the final amount after 10 years, we use the formula below.
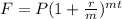
where:
P = principal = $20,000
r = interest rate = 0.055
m = compounding period = 4
t = time = 10 years
Let's plug into the formula the values of each variable.
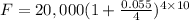
Solve for F.
a. Add the terms inside the parenthesis and multiply the exponents outside.
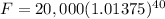
b. Apply the exponent.
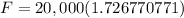
c. Multiply the two numbers.
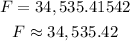
Answer:
After 10 years, there will be $34,535.42 available.