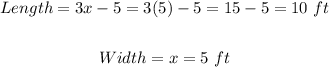Question

The length of a rectangle is 5 ft less than three times the width, and the area of the rectangle is 50 ft². Find the dimensions of the rectangle.

Answer 1

Length = 10 ft

Width = 5 ft

Step-by-step explanation

Area of the rectangle given = 50 ft²

Let the width of the rectangle be x

So this means the length of the rectangle will be 3x - 5

What to find:

The dimensions of the rectangle.

Step-by-step solution:

Area of a rectangle = length x width

i.e A = L x W

Put A = 50, L = 3x - 5, W = x into the formula.

`\begin{gathered} 50=(3x-5)x \\ 50=3x^2-5x \\ 3x^2-5x-50=0 \end{gathered}`

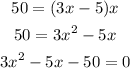
The quadratic equation can now be solve using factorization method:

`\begin{gathered} 3x^2-5x-50=0 \\ 3x^2-15x+10x-50=0 \\ 3x(x-5)+10(x-5)=0 \\ (3x+10)(x-5)=0 \\ 3x+10=0\text{ }or\text{ }x-5=0 \\ 3x=-10\text{ }or\text{ }x=5 \\ x=-(10)/(3)\text{ }or\text{ }x=5 \end{gathered}`

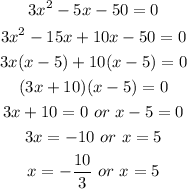
Since the dimension can not be negative, hence the value of x will be = 5.

Therefore, the dimensions of the rectangle will be:

`\begin{gathered} Length=3x-5=3(5)-5=15-5=10\text{ }ft \\ \\ Width=x=5\text{ }ft \end{gathered}`