Question

If c = 13 and angle B = 25degrees, find a.BсAСьa = [ ? ]Round to the nearest tenth.Enter

Answer 1

To determine the length of side "a", given that we know the length of the hypothenuse (side c) and the measure of angle B, you have to apply the trigonometric ratio cosine. Which is defined as:

`\cos \theta=(adjacent)/(hypothenuse)`

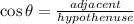
"θ" represents the angle, for our triangle it is ∠B

"adjacent" represents the side next to the angle, for our triangle, it is "side a"

"hypothenuse" is the longest side of the triangle, in this exercise, it is "side c"

Replace the expression with the known measures:

`\cos 25=(a)/(13)`

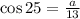
Multiply both sides by 13 to determine the value of 13

`\begin{gathered} 13\cdot\cos 25=13\cdot(a)/(13) \\ 11.78=a \\ a\approx11.8 \end{gathered}`

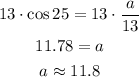
a= 11.8 units