Question

Find the mean, median, and mode of the set of values.

Answer 1

From the table for the data below,

The mean is calculated as

Hence the mean is 12.56 to two decimal places

The median. To get this, we summ the frequencies and divide by 2.

From the table, the total frequency is 57

`(57)/(2)=28.5\text{ }`

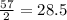
So we add the frequencies to see where 28.5 falls, we have

`\begin{gathered} 6+10+10=26_{} \\ 26+17=43,\text{ which is already above 28.5} \end{gathered}`

So the median lies in the part where we reached a frequency of 17. Tracing this to the ages in years (x), we get 13.

Hence the median is 13

The mode is the age in years (x) with the highest frequency. The one with the highest frequency is 13 with a frequency of 17.

Hence the mode is 13