We can decompose the figure in structures such that we can calculate the area of each structure.
Then, we have 3 rectangles, two triangles and a semicircle. The semicircle has diameter equals to
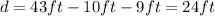
Then, the radius is equal to r=12ft.
We divide the figure in 6 different structures:
Structures I and V are triangles, so their area is

Structures II, III and IV are rectangles, so their area is

Structure VI is a semicircle, so the area is
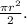
All the areas are in squared feet.
Structure I (b=10, h=48-37=11)
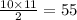
Structure II (a=37, b-10)

Structure III (a=38-12=26, b=43-10-9=24)
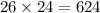
Structure IV (a=32, b=9)

Structure V (b=9, h=40-32=8)
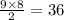
Structure VI (r=12)
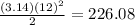
Then, we can obtain the total area adding all the area of the structures.
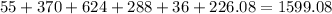
So, the total area is 1599.08 squared feet.