Question

Order these numbers from least to greatest. -6.44, 12/50, 0.2, -40.

Answer 1

To answer this question, we need to take into account that negative numbers are always lesser than a positive number, and, between two negative numbers, the one that has the greatest distance from 0 is lesser than the other negative number.

We have the numbers:

`-6.44,(12)/(50),\bar{0.2},-\sqrt[]{40}`

With the help of a calculator, we can find the value of all these numbers in decimal expression:

`(12)/(50)=(6)/(25)=0.24`

The number above is a terminating decimal. Only have two decimals.

`\bar{0.2}=0.222222222222\ldots`

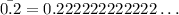
The latter is a periodic decimal number.

`-\sqrt[]{40}=-6.32455532034`

Now, we can observe the negative numbers:

`-6.44,-\sqrt[]{40}=-6.32455532034`

The number with the greatest absolute value, that is, with the greatest distance from 0 is -6.44, since:

`|-6.44|=6.44,|-6.32455532034|=6.32455532034`

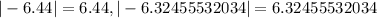
Therefore, we have the least number is -6.44, then -√40.

Now, which one is the greatest?:

`(12)/(50)=0.24,\bar{0.2}=0.222222222\ldots`

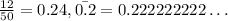
We can apply the same here. The one with the greatest absolute value is 0.24.

Therefore, to order these numbers from least to greatest is:

`-6.44<-\sqrt[]{40}<\bar{0.2}<0.24`