let x, y, z be the three test scores
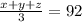
y is the median, y = 90
If the range is 6, then;
z - x = 6
Make z subject of formula from z - x = 6
z = 6+ x
substitute y =90 and z = 6+ x into our first equation and then solve for x
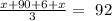
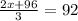
Multiply bothside by 3
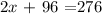
subtract 96 from bothside

Divide bothside by 2
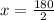
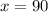
substitute x =90 into z = 6+ x
z = 6 + 90 =96
The three test scores are;
90, 90, 96