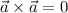Question

Grade 12 vectors Part 1 Q2Items a), b) and c)

Answer 1

By definition, the vectorial product of two vectors with the following coordinates:

`\begin{gathered} \vec{u}=x_1\hat{i}+y_1\hat{j}+z_1\hat{k} \\ \vec{v}=x_2\hat{i}+y_2\hat{j}+z_2\hat{k} \end{gathered}`

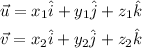
The vectorial product between those two vectors is given by the following determinant:

`\begin{gathered} \vec{u}*\vec{v}=\det\begin{bmatrix}{\hat{i}} & {\hat{j}} & {\hat{k}} \\ {x_1} & {y_1} & {z_1} \\ {x_2} & {y_2} & {z_2}\end{bmatrix} \\ =(y_1z_2-y_2z_1)\hat{i}+(x_2z_1-x_1z_2)\hat{j}+(x_1y_2-x_2y_1)\hat{k} \end{gathered}`

item a):

Using the previous definition in our problem, we have:

`\vec{k}*\vec{j}=\det\begin{bmatrix}{\hat{i}} & {\hat{j}} & {\hat{k}} \\ {0} & {0} & {1} \\ {0} & {1} & {0}\end{bmatrix}=(0-1)\hat{i}+(0-0)\hat{j}+(0-0)\hat{k}=-\hat{i}`

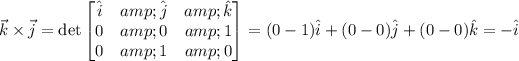
item b):

`(\hat{i}*\hat{j})*\hat{i}=\det\begin{bmatrix}{\hat{i}} & {\hat{j}} & {\hat{k}} \\ {1} & {0} & {0} \\ {0} & {1} & {0}\end{bmatrix}*\hat{i}=\hat{k}*\hat{i=\hat{j}}`

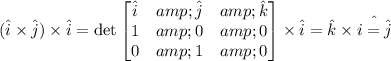
item c):

The vectorial product of a vector and itself is always equal to zero.

`\vec{a}*\vec{a}=0`