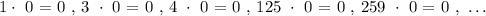We will address different properties that are applied to integers.
Commulative property:
The commulative property states that if you change the order of integers while applying the basic mathematical operations of ( Addition and Multiplication ) the answer will remain unchanged. We will illustrate this with help of an example as follows:

We tried changing the order of real numbers used in the two basic operations. We saw that the answer of each remain unchanged if we changed the order. Hence, Commulative property.
Associative property:
Refers to grouping of real number by adding paranthesis ( ) around a set of operations in a bigger chain of operations. So the property asserts that the choice of grouping the smaller sets does not affect the final answer. We will illustrate this with help of an example as follows:
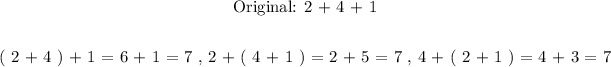
We made three combinations for selecting a smaller operations within a larger chain operation of addition. We grouped a pair of real numbers using parenthesis and resolved the parenthesis first then applied the last operation in each of the 3 cases illustrated above.
Identity property:
This property is divided into properties of addition and multiplication, where the identity is a real number ( 0 or 1 ) respectively. Both types of identity property are illustrated below as follows:

Both the identity property leaves to the same conclusion i.e any "number" added to (0) is always the " number ". Any "number" multiplied with digit ( 1 ) is the "number" itself.
Multiplication property of zero:
This property states that any real or imaginary number multiplied with ( 0 ) always results in 0. Illustrated below: