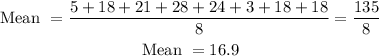Question

Find the mean, median, and mode of the list of values. Round to the nearest tenth if necessary.5, 18, 21, 28, 24, 3, 18, 18

Answer 1

Given the list of values:

`5,18,21,28,24,3,18,18`

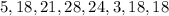
The corresponding frequency table is:

3: 1

5: 1

18: 3

21: 1

24: 1

28: 1

From this, we can say that the mode is:

`\text{Mode }=18`

There are 8 values. Ordering the list:

`3,5,18,18,18,21,24,28`

The position of the median can be calculated using the formula:

`P=(n)/(2)`

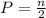
Where n is the number of values (n = 8). If p is a whole number, then the median is the semi-sum of the data at positions P and P+1. If it is not a whole number, the position of the median is int(P)+1, where int(P) is the integer part of P. Now, using the previous equation:

`P=(8)/(2)=4`

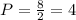
The values at positions 4 and 5 are 18 and 18, so the median is:

`\begin{gathered} \text{Median }=(18+18)/(2)=(36)/(2) \\ \Rightarrow\text{Median }=18 \end{gathered}`

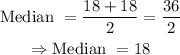
Finally, to find the mean (rounded to 1 decimal place), we use the value of n:

`\begin{gathered} \text{Mean }=(5+18+21+28+24+3+18+18)/(8)=(135)/(8) \\ \text{Mean }=16.9 \end{gathered}`