Question

1. Solve the following system by graphing. y=x^2+2x+7y=2x+72. The solution (s) is/ are ____.

Answer 1

`x=0,y=7`

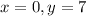
1) In this problem, we can write two t-tables. One t-table and find the roots of the quadratic equation, and the other t-table for the linear equation. We'll then trace the graph and check

2) We can plug random values into the equation so that we can get the values for y:

I) y=x²+2x+7

x|y

-1| y=6

0| 7

1| 10

(-1,6), (0,7), and (1,10)

`\begin{gathered} x^(2)+2x+7 \\ x=\frac{-2\pm\sqrt[]{4-28}}{2}=x_1=-1+\sqrt[]{6}i,x_2=-1-\sqrt[]{6}i \end{gathered}`

So as we can see, the complex roots tell us that the parabola does not cross the x-axis.

II) y=2x+7

x|y

-1| 5

0| 7

1| 9

(-1, 5), (0,7), and (1,9)

3) Now, we can plot both equations:

Note that the line and the parabola have one common point. So the answer to that Linear System is point (0,7) i.e., x=0 and y=7