Question

Determine the most specific name for quadrilateral JKLM if the coordinates of the vertices are:/(-4,6), K(-1,2), L(1,6), M(4,2)2124

Answer 1

To determine the type of quadrilateral, the first step is to plot the points and draw the quadrilateral JKLM:

The quadrilateral looks like a parallelogram, to determine if it is in fact a parallelogram we have to check if the following properties meet:

- The opposite sides are parallel, so JL || KM and JK || LM

- The opposite sides are equal JL=KM and JK=LM

The side JL is horizontal and parallel to the x-axis, you can determine this because both vertices have a y-coordinate at y=6.

The same happens with side KM, this side is also parallel to the x-axis, you can determine this over the graph but also because the coordinates of both vertices K and M have a y-coordinate at line y=2.

We can conclude that sides JL and KM are parallel.

To determine if the same happens with sides JK and LM, considering that they are sloping lines, we have to determine the slope of each side and compare them, if the slopes are equal, then the sides are parallel.

For this, we have to use the formula to calculate the slope of the line:

`m=(y_2-y_1)/(x_2-x_1)`

Where

(x₁,y₁) are the coordinates of one point of the line, in this case, the coordinates of one endpoint of the side.

(x₂,y₂) are the coordinates of a second point of the line, in this case, the coordinates of the other endpoint of the side.

The slope of the side JK

The endpoints are J(-4,6) and K(-1,2)

Replace the coordinates on the formula using K as (x₂,y₂) and J as (x₁,y₁).

`\begin{gathered} m=(2-6)/(-1-(-4)) \\ m=(-4)/(3) \end{gathered}`

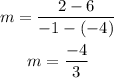
The slope of the side LM

The endpoints are L(1,6) and M(4,2).

Replace the coordinates on the formula, using M as (x₂,y₂) and L as (x₁,y₁).

`\begin{gathered} m=(2-6)/(4-1) \\ m=(-4)/(3) \end{gathered}`

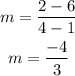
Both sides JK and LM have the same slope m=-4/3, which means that they are parallel.

So JK || LM

Next, we have to determine if the opposite sides are congruent. For this we need to use the formula to determine the distance between two points on the coordinate system:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_2)}`

Where

(x₁,y₁) are the coordinates of one endpoint of the line.

(x₂,y₂) are the coordinates of the second endpoint of the line.

For JL

Endpoints J (-4,6) and L (1,6)

Replace the coordinates on the formula to determine the length of the line:

`\begin{gathered} JL=\sqrt[]{(1-(-4))^2+(6-6)^2} \\ JL=\sqrt[]{(5)^2+(0)^2} \\ JL=\sqrt[]{25} \\ JL=5 \end{gathered}`

For KM

Endpoints K (-1,2) and M (4,2)

`\begin{gathered} KM=\sqrt[]{(-1-4)^2+(2-2)^2} \\ KM=\sqrt[]{(-5)^2+(0)^2} \\ KM=\sqrt[]{25} \\ KM=5 \end{gathered}`

Sides JL and KM have a length of units, so both sides are equal.

For JK

Endpoints J(-4,6) and K(-1,2)

`\begin{gathered} JK=\sqrt[]{(-1-(-4))^2+(2-6)^2} \\ JK=\sqrt[]{(3)^2+(-4)^2} \\ JK=\sqrt[]{9+16} \\ JK=\sqrt[]{25} \\ JK=5 \end{gathered}`

For LM

Endpoints L(1,6) and M(4,2)

`\begin{gathered} LM=\sqrt[]{(4-1)^2+(2-6)^2} \\ LM=\sqrt[]{(3)^2+(-4)^2} \\ LM=\sqrt[]{9+16} \\ LM=\sqrt[]{25} \\ LM=5 \end{gathered}`

Sides JK and LM have the same length, they are congruent.

The opposite sides JL and KM are parallel and equal.

The opposite sides JK and LM are parallel and equal.

Looking at the graph, the angles are not right angles.

You can conclude that the quadrilateral JKLM is a parallelogram.