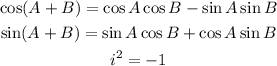Question

Perform the indicated operation:10{cos(12)+i sin(12)]*14[cos \left(88)+i sin (88)]Give your answer in polar form:

Answer 1

`140\lbrack\cos 100^0+i\sin 100^0\rbrack`

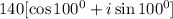
Step-by-step explanation:

Given the operations

`$10\mleft[\cos \mleft(12^(\circ)\mright)+i\sin \mleft(12^(\circ)\mright)\mright]^*14\mleft[\cos \mleft(88^(\circ)\mright)+i\sin \mleft(88^(\circ)\mright)\mright]$$$`

First, we distribute each of the number outside the brackets to obtain:

`$=\lbrack10\cos (12^(\circ))+10i\sin (12^(\circ))\rbrack\lbrack14\cos (88^(\circ))+14i\sin (88^(\circ))\rbrack$`

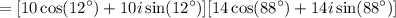
Next, we expand:

`$=10\cos (12^(\circ))\lbrack14\cos (88^(\circ))+14i\sin (88^(\circ))\rbrack+10i\sin (12^(\circ))\lbrack14\cos (88^(\circ))+14i\sin (88^(\circ))\rbrack$`

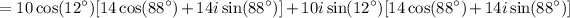
We open the brackets:

`$=140\cos (12^(\circ))\cos (88^(\circ))+140i\sin (88^(\circ))\cos (12^(\circ))+140i\sin (12^(\circ))\cos (88^(\circ))+140i^2\sin (12^(\circ))\sin (88^(\circ))$`

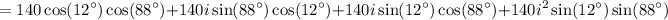
Finally, we collect like terms and simplify:

`\begin{gathered} $=140\cos (12^(\circ))\cos (88^(\circ))+140i\sin (88^(\circ))\cos (12^(\circ))+140i\sin (12^(\circ))\cos (88^(\circ))-140^{}\sin (12^(\circ))\sin (88^(\circ))$ \\ =140\cos (12^(\circ))\cos (88^(\circ))-140^{}\sin (12^(\circ))\sin (88^(\circ))+140i\sin (88^(\circ))\cos (12^(\circ))+140i\sin (12^(\circ))\cos (88^(\circ)) \\ =140\cos (12^0+88^0)+140i(\sin (88^0+12^0) \\ =140\lbrack\cos 100^0+i\sin 100^0\rbrack \end{gathered}`

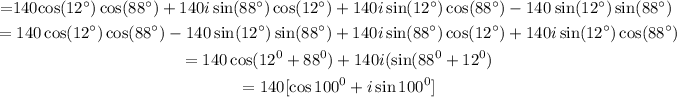
Note the following:

We applied the trigonometric identities below:

`\begin{gathered} \cos (A+B)=\cos A\cos B-\sin A\sin B \\ \sin (A+B)=\sin A\cos B+\cos A\sin B \\ i^2=-1 \end{gathered}`