Question

If you hold a 28.02 cm² square plane mirror 40.26 cm from your eyes and can just see the full length of a 8.9 m flag pole behind you, how far are you from the pole?

Answer 1

66.8 m

Explanation:

Given:

Area of mirror = 28.02 cm²

We make a sketch of the situation in order to solve the problem:

We calculate the height as follows:

`\begin{gathered} h=√(28.02)=5.3\text{ cm} \\ \\ \text{ therefore:} \\ \\ AC=(5.3)/(2)=2.65\text{ cm } \\ \\ \text{ For ABC:} \\ \\ \tan\theta=(2.65)/(40.26) \end{gathered}`

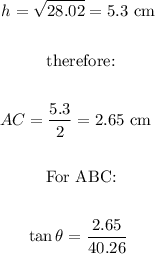
Now, we determine for AEF that it has the same angle as ABC, like this:

`\begin{gathered} \tan\theta=(EF)/(EA)=((890)/(2)-2.65)/(d) \\ \\ \text{ Therefore:} \\ \\ (2.65)/(40.26)=((890)/(2)-2.65)/(d) \\ \\ \text{ we solve for d:} \\ \\ \:d=(40.26)/(2.65)\cdot\left((890)/(2)-2.65\right)\: \\ \\ d=6720.38\text{ cm} \\ \\ d=67.2\text{ m} \\ \\ \text{ Therefore:} \\ \\ D=67.2-0.4026=66.7974\equiv66.8\text{ m} \end{gathered}`

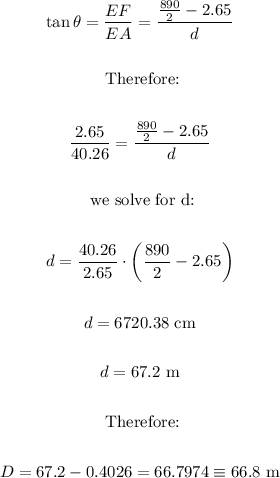
It is located 66.8 meters from the pole