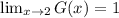In this case, notice that the graph of G(x) approximates to 1 when x goes to 2 from the left, and also the graph approximates to 1 when x goes to 2 from the right, thus, we have the following limits:
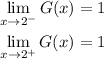
since both limits are equal, we have that the limit of G(x) when x goest to 2 is: