Question

I am having a hard time solving this practice problem from my ACT prep guide

Answer 1

To start evaluating the given expression, first, replace the pi value with 180 degrees.

`\tan (-(2\pi)/(3))=\tan (-(2*180)/(3))=\tan (-(360)/(3))=\tan (-120)`
`\sin (7\pi)/(4)=\sin ((7*180)/(4))=\sin (1260)/(4)=\sin 315`
`\sec (-\pi)=\sec (-180)=(1)/(\cos (-180))`

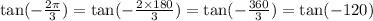
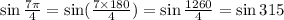
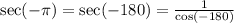
Now that we have converted the radian angles in degrees, let's get the numerical value of each function using calculator.

`\begin{gathered} \tan (-120)=\sqrt[]{3} \\ \sin 315=-\frac{\sqrt[]{2}}{2} \\ (1)/(\cos (-180))=-1 \end{gathered}`

From that, we can say that the given expression is equal to:

`\begin{gathered} \frac{\sqrt[]{3}}{-\frac{\sqrt[]{2}}{2}}-(-1) \\ =(\frac{\sqrt[]{3}}{1}*-\frac{2}{\sqrt[]{2}})+1 \\ =\frac{-2\sqrt[]{3}}{\sqrt[]{2}}+1 \\ \text{Rationalize.} \\ =(\frac{-2\sqrt[]{3}}{\sqrt[]{2}}*\frac{\sqrt[]{2}}{\sqrt[]{2}})+1 \\ =-\sqrt[]{6}+1^{}^{} \end{gathered}`

The given expression is equal to -√6 + 1 or 1 - √6.