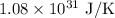Question

The Sun radiates energy at the rate of 3.80 ✕ 1026 W from its 5500°C surface into dark empty space (a negligible fraction radiates onto Earth and the other planets). The effective temperature of deep space is −270°C. (Due to the sensitive nature of the calculations, use T(K) = T(°C) + 273.15.(a) What is the increase in entropy (in J/K) in one day due to this heat transfer?

Answer 1

Given:

The sun radiates energy at a rate of

`W=3.80*10^(26)\text{ W}`

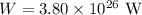
The temperature in the empty space is,

`\begin{gathered} T_H=5500+273 \\ =5773\text{ K} \end{gathered}`

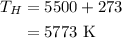
The temperature at the deep space is,

`\begin{gathered} T_c=-270+273 \\ =3\text{ K} \end{gathered}`

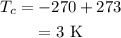
To find:

the increase in entropy (in J/K) in one day

Step-by-step explanation:

The value of heat is,

`\begin{gathered} Q_H=Q_c=Q=3.80*10^(26)*24*3600 \\ =3.28*10^(31)\text{ J} \end{gathered}`

The change in entropy is,

`\begin{gathered} \Delta s=-(Q_H)/(T_H)+(Q_c)/(T_c) \\ =-(3.28*10^(31))/(5773)+(3.28*10^(31))/(3) \\ =1.08*10^(31)\text{ J/K} \end{gathered}`

Hence, the increase in entropy is

`1.08*10^(31)\text{ J/K}`