Question

Identify the equation in slope-intercept form for the line containing the point (0, 7) and perpendicular to y=-5/4x + 11/4.

Answer 1

Given the equation

`y=-(5)/(4)x+(11)/(4)`

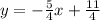
Here, the radient is;

`m=-(5)/(4)`

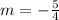
Since the line in question is perpendicular to the given line,

The product of their gradient mst be -1

`\begin{gathered} m_1* m=-1 \\ \\ \Rightarrow m_1=-(1)/(m) \\ \\ \text{ since }m=-(5)/(4) \\ \\ \Rightarrow m_1=-(1)/(-(5)/(4))=(4)/(5) \end{gathered}`

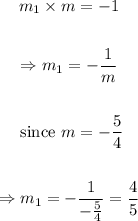
Therefore, the gradient of the line in questin is 4/5

Since the line passes trough the poinyt (0, 7)

`\begin{gathered} \Rightarrow(y_-y_1)/(x-x_1)=m \\ \\ \Rightarrow(y-7)/(x-0)=(4)/(5) \\ \\ \Rightarrow(y-7)/(x)=(4)/(5) \\ \\ \Rightarrow y-7=(4)/(5)x \\ \\ \Rightarrow y=(4)/(5)x+7 \end{gathered}`

Hence, the correct option is A.