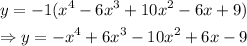The given polynomial is said to have a degree of 4. It has zeros 3 (multiplicity two) and i (multiplicity one) and contains the point (0,-9).
It is required to find the equation of the polynomial.
Recall the Complex Conjugate Theorem: A polynomial function or a polynomial equation with real coefficients that has a+bi as a complex zero, with b not zero, also has a-bi as a zero.
Since i is a zero of the polynomial, its conjugate -i is also a zero.
Hence, the zeros of the polynomial are 3,i,-i.
Recall from the factor theorem that if k is a zero of a polynomial with multiplicity m, then the expression,
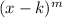
is a factor of the polynomial.
It follows that the polynomial has factors:
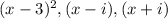
Hence, the polynomial can be written as a product of its factors and a real constant, a:

Simplify the product on the right as follows:
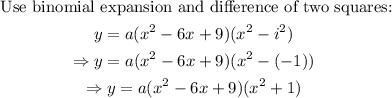
Expand the expression further:
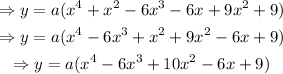
Since it is given that the polynomial contains the point (0,-9), substitute (x,y)=(0,-9) into the equation to find the value of a:
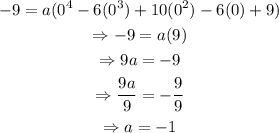
Substitute a=-1 back into the equation.
Hence, the required polynomial is: