Question

Is Lydia correct if not what is the correct equation?

Answer 1

Notice that triangles XYZ and WYZ are congruent because of the SAS postulate.

Then,

`\begin{gathered} 5x-5=3x+9 \\ \text{and} \\ 4x+6=5x-1 \end{gathered}`

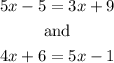
Because the pairs of corresponding sides are XZ-ZW and XY-YW.

Therefore, we cannot conclude that

`XY=ZW`

On the other hand, the algebra used by Lydia has no mistakes.

`\begin{gathered} 4x+6=3x+9 \\ \Rightarrow-3x+4x+6=-3x+3x+9 \\ \Rightarrow x+6=9 \\ \Rightarrow x=3 \end{gathered}`

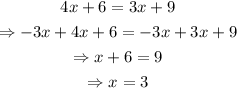
So, Lydia is incorrect when setting the equation, the algebraical operations are correct.

The two valid equations are:

`\begin{gathered} 5x-5=3x+9 \\ or \\ 4x+6=5x-1 \end{gathered}`

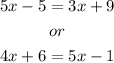
We can even combine both equations and obtain

`\begin{gathered} 4x+6-4=3x+9 \\ \Rightarrow4x+2=3x+9 \end{gathered}`

The answer is:

Lydia is wrong because the initial equation is false. The two possible equations are 5x-5=3x+9 or 4x+6=5x-1.