If you don’t need further explanation on this question, we can end the session. Remember the answer of this question will be on your profile once we finish the session. I’d really appreciate you letting me know how I did by rating our session after you exit. Thanks and have a great day!
To find the inverse of a function, we need to replace f(x) for y and switch every x for a y, and every y for a x:
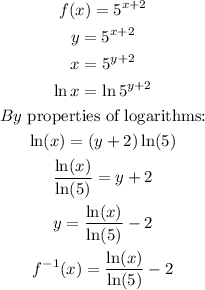
1. The graph of f^-1(x) would be:
2. Domain of a function is all the set x-values or input values of a function, so in this case:
As we can see in the graph the function goes from (0, ∞), then its domain:
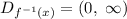
3. Range is the set of y-values that the function can take or output values, in this case, we can see it goes from 0 to -∞, then its range would be:
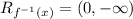
4. In the graph, we can see that from 0 to ∞, the function is increasing.
5. Vertical asymptotes are vertical lines which correspond to the zeroes of the denominator of a rational function, we can see that the asymptote would be x=0.