We are asked to determine the net rate of radiation of a roof given its area and its emisivity. To do that we will use the following formula:

Where:

The Stefan-Boltzmann's constant is given by:
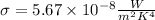
Now, we need to convert the temperature to Kelvin. To do that we use the following:
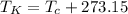
Where:
For the 33°C we have:

For the 14°C:
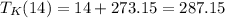
Now, we substitute the values:
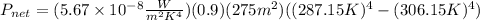
Solving the operation:
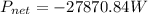
Therefore, the net rate of radiation is -27870.84 Watts.