Question

Write the equation of the line that passes through the point (-7, -1) and isperpendicular to x = -3y+6. Write your answer in slope-intercept form y = mx + b

Answer 1

If two lines are perpendicular, the multiplication of the slopes is equal to -1.

So, the line x = -3y + 6 can be written as:

`\begin{gathered} x=-3y+6 \\ x-6=-3y \\ (x-6)/(-3)=y \\ (-1)/(3)x+2=y \end{gathered}`

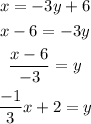
So, the slope is -1/3. It means that the slope of the perpendicular line is:

`\begin{gathered} (-1)/(3)\cdot m=-1 \\ -m=-3 \\ m=3 \end{gathered}`

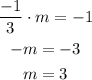
Then, with a point (x1, y1) and a slope m, we can find the equation of the line as:

`y-y_1=m(x-x_1)`

Replacing, m by 3 and (x1, y1) by (-7,-1), we get:

`\begin{gathered} y-(-1)=3(x-(-7)) \\ y+1=3(x+7) \\ y+1=3x+21 \\ y=3x+21-1 \\ y=3x+20 \end{gathered}`

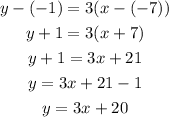
Answer: y = 3x + 20