Step 1: Given the equation
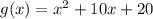
Step 2: Evaluate g(-9).
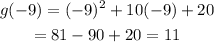
Step 3: Evaluate g(0)
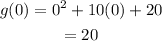
Step 4: Given an interval [-9 , 0], the rate of change formula is
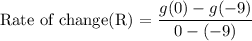
Step 5: Substitute for the values of g(0) and g(-9)
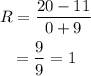
Therefore, the average rate of change for the function over the interval [-9,0] is 1