Suppose Dee invests "x" dollars in 9.5% interest paying account and "y" dollars in 4% interest paying account.
Total Invested = $ 10,125
Thus, we can write:
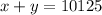
Simple Interest earned is given by the formula
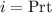
Where
i is the interest earned,
P is the amount invested in the account,
r is the rate of interest in decimal
t is the time in years
• For 9.5% account, we can say that the interest earned is:
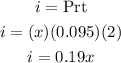
• For 4% account, we can say that the interest earned is:
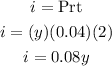
The total interest earned is 1580, thus we can form the second equation:
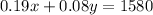
Solving the first equation for x gives us:
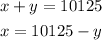
Now, we substitute this into the second equation and solve for y first:

Using this value of y, we can easily figure out the value of x.
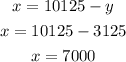
So,
Dee invested $7000 in 9.5% account and $3125 in 4% account.