Question

Dee invested a total 10,125 in two accounts pay 9.5% and 4% simple interest. if a total return at the end of the two years was 1580, how much did she invest in each account?

Answer 1

Suppose Dee invests "x" dollars in 9.5% interest paying account and "y" dollars in 4% interest paying account.

Total Invested = $ 10,125

Thus, we can write:

`x+y=10125`

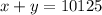
Simple Interest earned is given by the formula

`i=\text{Prt}`

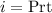
Where

i is the interest earned,

P is the amount invested in the account,

r is the rate of interest in decimal

t is the time in years

• For 9.5% account, we can say that the interest earned is:

`\begin{gathered} i=\text{Prt} \\ i=(x)(0.095)(2) \\ i=0.19x \end{gathered}`

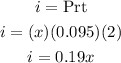
• For 4% account, we can say that the interest earned is:

`\begin{gathered} i=\text{Prt} \\ i=(y)(0.04)(2) \\ i=0.08y \end{gathered}`

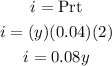
The total interest earned is 1580, thus we can form the second equation:

`0.19x+0.08y=1580`

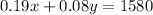
Solving the first equation for x gives us:

`\begin{gathered} x+y=10125 \\ x=10125-y \end{gathered}`

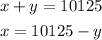
Now, we substitute this into the second equation and solve for y first:

`\begin{gathered} 0.19x+0.08y=1580 \\ 0.19(10125-y)+0.08y=1580 \\ 1923.75-0.19y+0.08y=1580 \\ 0.19y-0.08y=1923.75-1580 \\ 0.11y=343.75 \\ y=3125 \end{gathered}`

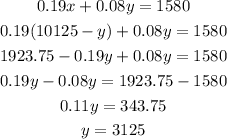
Using this value of y, we can easily figure out the value of x.

`\begin{gathered} x=10125-y \\ x=10125-3125 \\ x=7000 \end{gathered}`

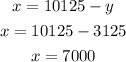
So,

Dee invested $7000 in 9.5% account and $3125 in 4% account.