Question

How would I calculate the radian measure of 225 degree angle. (in any method).

Answer 1

Step-by-step explanation:

The measure of an angle is determined by the amount of rotation from the initial side to the terminal side. In radians, one complete counterclockwise revolution is 2π.

2π is equivalent to 360 degrees.

this is equivalent to saying:

`2\pi=360^(\circ)`

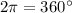
then

`\pi=180^(\circ)`

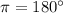
Taking into account this information, algebraically to convert from degrees to radians we can multiply the degrees by π/180 radians.

In this case, we obtain:

`(225^(\circ))((\pi)/(180^(\circ))\text{ rad})=\text{ }(5)/(4)\pi`

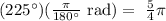
Now, graphically note that 225 degrees can be represented on the trigonometric circle in the following way:

Then, we can conclude that the correct answer is:

Answer:

`(5)/(4)\pi`

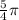
and this angle can be represented in the following trigonometric circle: