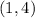Given the System of Equations:
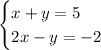
Part A
You can sketch the graph of the System of Linear Equations as follows:
1. Find the x-intercept of the first line by substituting this value of "y" into the first equation and solving for "x" (because the y-value is zero when the line intersects the x-axis):

Then, you get:

2. Find the y-intercept of the first line by substituting this value of "x" into the first equation and solving for "y" (because the x-value is zero when the line intersects the y-axis):

Then:

Now you know that the first line passes through these points:
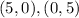
3. Find the x-intercept of the second line applying the same procedure used with the first line:
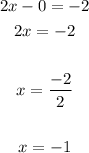
4. Find the y-intercept of the second line applying the same procedure used with the first line:
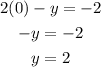
Now you know that the second line passes through these points:
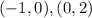
5. Graph both lines in the same Coordinate Plane:
Part B
By definition, when two lines of a System of Equations intersect each other, the system has one solution. The solution is the point of intersection between the lines. In this case, it is:
Hence, the answers are:
Part A
Part B