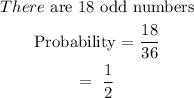Question

Two dice are rolled; find the favor of rolling a sum:a. Equaling 8b. greater than 6c. Less than or equal to 9d. that is an odd number

Answer 1

When two dice are rolled, there are 36 possibilities. These can be found by calculating the number of counts.

We are required to find the favor of rolling a sum, which is similar to saying the probability of rolling a given sum.

Recall that the probability of an event occurring is given as:

`\text{Probability = }\frac{Number\text{ of required outcomes}}{\text{Total Number of possible outcomes}}`

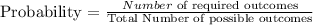
(a) Sum equaling 8

`\text{Probability = }(5)/(36)`

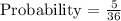
(b) Greater than 6

(c) Less than or equal to 9

`\begin{gathered} \text{Probability = 1 - Probability of a sum greater than 9} \\ =\text{ 1 - (Probability of 10 + Probablity of 11 + Probability of 12)} \\ =\text{ 1 - }(6)/(36) \\ =\text{ }(30)/(36) \\ =\text{ }(5)/(6) \end{gathered}`

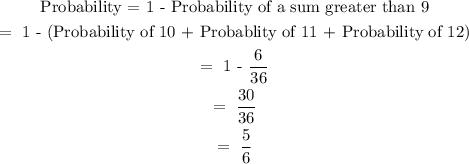
(d) That is an odd number

Odd numbers are 1, 3 , 5 , ...

`\begin{gathered} There\text{ are 18 odd numbers} \\ \text{Probability = }(18)/(36) \\ =\text{ }(1)/(2) \end{gathered}`