Answer:
Concept:
The question will be solved using the empirical rule below
The Empirical Rule states that 99.7% of data observed following a normal distribution lies within 3 standard deviations of the mean. Under this rule, 68% of the data falls within one standard deviation, 95% percent within two standard deviations, and 99.7% within three standard deviations from the mean.
a) To figure out the percentage of students that scored between 34 and 60, we will use the principle below
As the scores are normally distributed so, according to empirical rule the percentage of data falls within one,two and three standard deviations are 68%,95% and 99.7% respectively.
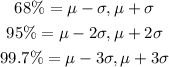
Where the mean and standard deviation given are
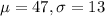
By substituting the values, we will have
![\begin{gathered} 68\operatorname{\%}=\mu-\sigma, \mu+\sigma \\ 68\%=47-13=34 \\ =47+13=60 \end{gathered}]()
Hence,
Approximately __68%__ of the students scored between 34 and 60.
B)
Approximately 99.7% of the students scored between __ and ___
To figure out the values, we will use the formula below
![99.7\operatorname{\%}=\mu-3\sigma, \mu+3\sigma]()
By substituting the values, we will have
![\begin{gathered} 99.7\operatorname{\%}=\mu-3\sigma, \mu+3\sigma \\ \mu-3\sigma=47-3(13)=47-39=8 \\ \mu+3\sigma=47+3(13)=47+39=86 \end{gathered}]()
Hence,
The final answer is
Approximately 99.7% of the students scored between _8_ and _86__