Question

An Aircraft factory manufactures airplane engines. The unit cost C ( the cost in dollars to make each airplane engine) depends on the number of engines made. If x engines are made, then the unit cost is given by the function C(x)=0.6^2-324x+56,258. What is the minimum unit cost? Do not round your answer.

Answer 1

We have that the unit cost is given by a parabola, and the leading coefficient is given by 0.6 (it is positive), then, we have a minimum in the shape of the parabola.

A way to find the minimum is to find the vertex of the parabola (in this given case, the vertex is the minimum point) which coordinates are as follows:

`x_v=-(b)/(2a),y_v=c-(b^2)/(4a)`

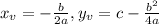
Since we need to find the minimum unit cost, we need to find the value for y. Then, we have:

`0.6x^2-324x+56258`

a = 0.6

b = -324

c = 56258

Then

`y_v=56258-((-324)^2)/(4\cdot(0.6))\Rightarrow y_v=12518`

Therefore, the minimum unit cost is equal to $12,518.