INFORMATION:
We know that the function that describes Katie's parabolic trajectory is
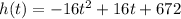
And we must graph it, identifying Katie's start and end points
STEP BY STEP EXPLANATION:
Since we have a parabola, we can calculate the vertex to graph it
The formula for the vertex is
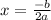
In this case, a = -16 and b = 16
Now, replacing in the formula
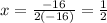
Now, we must replace t = 1/2, to find the coordinate of the vertex
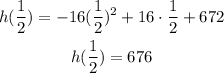
Then, the coordinate of the vertex is (1/2, 676)
Now, we can find the x intercepts if we equal the function to 0 and solve for t
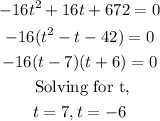
Now, knowing the vertex and the x-intercepts we can graph the function
In the graph we take the positive part of the parabola because t (x-axis) represents time and the time must be positive
The end point would be when h(t) = 0
ANSWER: