Answer:
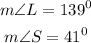
Explanations:
If the sum of the measures of any two supplementary angles is 180 degrees and m
 Also, if the measure of < L is sixty-six degrees less than five times the measure of < S, then:
Also, if the measure of < L is sixty-six degrees less than five times the measure of < S, then:

Substitute equation 2 into equation 1 to have:

Simplify the result to have:

Add 66 to both sides of the resulting equation:
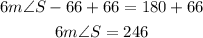
Divide both sides of the equation by 6
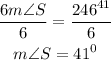
Get the measure of < L. Recall that:
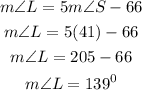
Hence the measure of < L is 139 deg. while the measure of