Answer:
The linear function f with the given values f(-1) = -6, f(4) = -6 is:
f(x) = -6
Step-by-step explanation:
The given values are:
f(-1) = -6, f(4) = -6
This can be interpreted as:
x₁ = -1, f₁ = -6, x₂ = 4, f₂ = -6
The equation of a line is written as:
f - f₁ = m(x - x₁)
where m is the slope and is given by the formula:
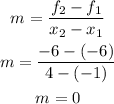
Substitute f₁ = -6, m = 0, and x₁ = -1 into the equation f - f₁ = m(x - x₁)
f - (-6) = 0(x - (-1)
f + 6 = 0(x + 1)
f + 6 = 0
f = -6
The linear function f with the given values f(-1) = -6, f(4) = -6 is:
f(x) = -6