Question

Select the correct answer.Consider the functions below.f(x) = 8x^2 + x + 3g(x) = 4^x– 1h(x) = 3x + 6. which of the following statements is true?

Answer 1

Given:

`\begin{gathered} f(x)=8x^2+x+3 \\ g(x)=4^x-1 \\ h(x)=3x+6 \end{gathered}`

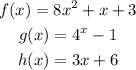
a) the average rate of change in the interval [3,5] is,

`\begin{gathered} f_(avg)=(f(5)-f(3))/(5-3) \\ f_(avg)=(8(5^2)+5+3-(8(3^2)+3+3))/(2) \\ f_(avg)=(130)/(2)=65 \end{gathered}`

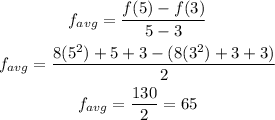
Also,

`\begin{gathered} g_(avg)=(g(5)-g(3))/(5-3) \\ g_(avg)=(4^5-1-(4^3-1))/(2) \\ g_(avg)=480 \end{gathered}`

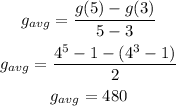
And,

`\begin{gathered} h_(avg)=(h(5)-h(3))/(5-3) \\ h_(avg)=(3(5)+6-(3(3)+6)))/(2) \\ h_(avg)=(6)/(2)=3 \end{gathered}`

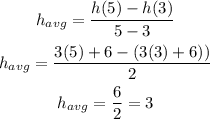
Option a) is not correct. because the average rate of change of g and h is not more than f.

b) for the interval [0,2],

`\begin{gathered} f_(avg)=(f(2)-f(0))/(2-0) \\ =(8(2^2)+2+3-(3))/(2) \\ =17 \\ g_(avg)=(g(2)-g(0))/(2-0) \\ =(4^2-1-(0-1))/(2) \\ =8 \\ h_(avg)=(h(2)-h(0))/(2-0) \\ =(3(2)+6-(6))/(2) \\ =3 \end{gathered}`

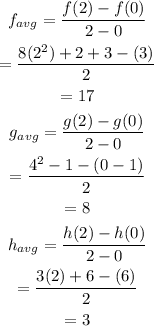
Option b) is also not correct.

when x approaches to infinity, the values of g(x) and h(x) exceeds the values of f(x).

Answer: option d)