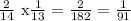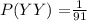SOLUTION:
Step 1:
A bag has 14 marbles, all identical except for their color.
There are 7 red marbles, 5 blue marbles, and 2 yellow marbles.
If you draw two marbles from the bag WITHOUT replacement,
find the following probabilities:
7 red marbles , 5 blue marbles and 2 yellow marbles
Total = 7 + 5 + 2 = 14
( Without Replacement)
a.) P(RR) =
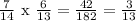
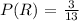
b.) P(RB) =
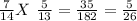
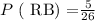
c.) P(RY) =
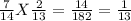
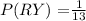
d.) P(BR) =
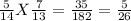
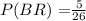
e.) P(BB) =
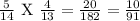
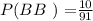
f.) P(BY) =
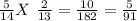
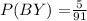
g.) P(YR) =
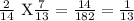
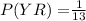
h.) P(YB) =
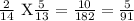
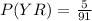
l) P(YY) =